
Günlerdir internette farklı kaynaklarda “Bu resimde kaç kare var?” sorusunu görmekteyim. Herkes farklı cevaplar vermiş, soru üzerinde tartışmalar almış başını gitmiş. Şimdi bütün bu gürüzgahın içinden çıkıp soruyu cevaplayalım istedim. Bütün düzgün iç içe olan “kaç kare var?” sorularının cevabını sizlerle paylaşacağım. Oturup her soru için teker teker kareleri sayma, acaba göremediğim başka kare var mıydı diye kafa patlatma deviri bu yöntemle sona erecek. 4x4lük kare için oturup saydınız diyelim. Peki soru satranç tahtası olsaydı da sayacak mıydık? 🙂 Bunun için matematiğin inceliklerinden faydalanmak en mantıklısı…
Matematik, problem çözme sanatıdır. Benzer tarzdaki sorular için geliştirilen çözüm yöntemleri vardır. Bu yöntemleri formül, fonksiyon veya metod olarak adlandırabiliriz. Biz de bu tip sorular için kendi yöntemimizi geliştireceğiz. Böylelikle kaç kare var soruları ister 3x3lük, isterse 8x8lik olsun tek bir formül uygulayarak çözebileceğiz!
Hızlı Giriş:
Öncelikle formülü vermek istiyorum. Daha sonra örneklerle yöntemimizi pekiştiririz.
Şekilde 4x4lük bir kare vardır. Bu karenin herbir kenarında 4 tane küçük kare olduğuna dikkat edin. Bize gerekli olan sayı da en büyük düzgün karenin kenarlarını oluşturan bu küçük karelerin sayısıdır.
Yapacağımız işlem 1’den başlayıp bu sayıya kadar olan sayıların karelerini toplamak olacaktır.
Çıkan sonuç bize şekilde kaç kare olduğunu verecektir.Örnekten devam edecek olursak bu sayı 4’dür.
Öyleyse,
[latex]1^2[/latex]+[latex]2^2[/latex]+[latex]3^2[/latex]+[latex]4^2[/latex]
bizi sonuca götürecektir. Bu işlemin sonucu:
1 + 4 + 9 + 16 = 30’dur.
Gördüğünüz gibi kareleri teker teker saymadan sonuca ulaştık. İnanmadıysanız siz saymaya başlayabilirsiniz. Daha sonra yazının devamını okuyarak daha kısa yöntemlerle her türlü kaç kare var soruna cevap bulabilirsiniz.
Bu işlemi matematikteki toplam sembolü olan Sigma ![]() ile gösterebiliriz.
ile gösterebiliriz.
Şöyleki:
Buradaki “n” değeri bizim büyük karenin bir kenarını oluşturan küçük karelerin sayısıdır. Örneğimize göre 4’dür. “k” değeri ise “n” değerine kadar 1’den başlayıp birer artarak devam eden değişkenimizdir. Örneğimize göre k değeri sırasıyla 1, 2, 3 ve 4 değerlerini alır.
Bu kısım biraz bilimsel gelebilir ama biraz daha sabrederseniz. Kısa bir formülle işi bağlayacağım 🙂
Her seferinde sayıların karelerini mi alacağız?
Diyelim ki bir satranç tahtasında kaç kare olduğunu bulacağız. Satranç tahtası 8×8’lik bir karedir. Bu durumda formülümüzü uyguladığımızda 1’den 8’e kadar olan sayıların karelerini alıp toplamamız gerekmektedir. Teker teker kareleri saymaktan daha kolay bir yöntem olduğu aşikardır. Aynı zamanda formülün doğru cevap garantisi vardır. Fakat daha kısa bir yöntem daha var.
Bu karelerin toplamı: 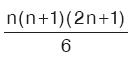 ‘ya eşittir.
‘ya eşittir.
Asıl formülün eşitliğini şöyle gösterebiliriz:
Sorumuza dönecek olursak; Satranç tahtası için “n” değerinin alacağı değer 8’dir. Bu durumda 8’i formülde yerine yazarsak
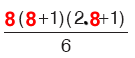 ‘dır. Buradan 8 x 9 x 17 / 6 = 204 sonucunu buluruz.
‘dır. Buradan 8 x 9 x 17 / 6 = 204 sonucunu buluruz.
Sonuç
Artık karelerin büyüklükleri bizim için bir problem olmaktan çıkmıştır. Kaç kare var soruları bizim için basit çarpma ve bölme işlemleri ile sınırlı kalmaktadır.
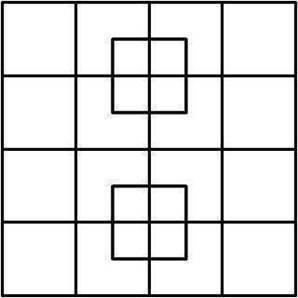
Yazımızı bir soruyla bitirelim. Aşağıdaki şekilde kaç kare vardır? Bakalım kaç kişi hala saymaya devam ediyor? 🙂
NOT: Sorunun cevabını yukarıdaki formül ile rahatlıkla bulabilirsiniz. Doğru cevabı bir sonraki yazımda paylaşacağım. Esenlikle kalınız.

 92306
92306 

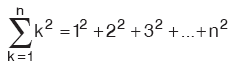
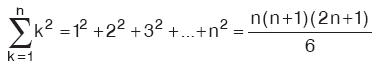









Hortlaşmış gibi olucam ama yazıyla olanıda sayarsak sonuç 31 çıkacaktır..
30
1+4+9+18+8=40
40 olabilir isterseniz yeni den okuyun
Aptalca bir cevap, çünkü 16 kare var , önce bir kare çizin ve ardında çizdiğiniz kareden kaç tane var bir bakınız, üst üste gelenlerine sayıyorsunuz, görünmeyen çizimizde kare çizimi olarak görüyorsunuz, siz görünenleri sayınız, görünmeyenleri değil
25
aslında orda 1 kare var
26 tane
Cevap 40
[4(4+1).(2.4+1)/6]+2.5=
[4.5.9/6]+10
30+10=40
Aslinda kare yok
Teşekkürler. Bu arada aynı formülü üçgen vb içinde kullanabilir miyiz?
18 dir